試験分析結果の活かし方
Utilizing Test Results Analysis
今回は、試験分析結果データの数値について、活かし方が分からないというお問い合わせをお客様から頂戴しましたので、その数値をどう現実的に活用するのかのセオリーについてご説明をさせていただきます。
【1】標準偏差(分散値の平方根)
「受験者データのばらつきを表す」とは一般的ですが、それってどういう意味?どう利用すればいいの?この点が最初の課題です。
この値で知っておくべきことは、「68%、95%ルール」です。
受験者のデータが正規分布の形で分散していると想定した場合、標準偏差をσで表すと±1σの範囲に、68.27%の人が分布しているという事を表し、±2σの範囲に、95.45%の人が分布しているという事を表します。
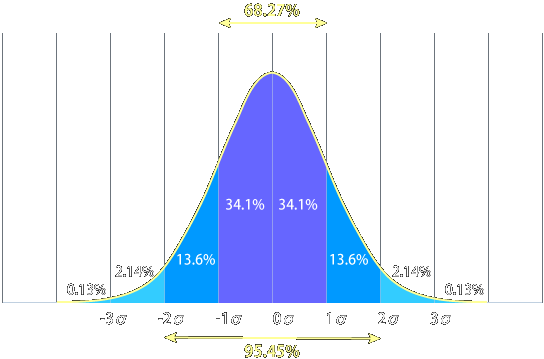
つまり標準偏差が例えば10という値で平均点が60点のテストの場合、±1σの範囲、50-70点の範囲に受験者の68%の人が分布している事になり、40-80点の範囲内に95%の人が分布しているという事になります。
これは、合格ラインの算定に用いる知識と言えます。例えば、平均点60点で標準偏差が10の場合に、70点を合格ラインにすると、合格者は(100%-68%)÷2=16%程度の人となります。合格者のライン算定の基準の一つの指標として何%くらいの人を合格させたいのかという考えがある場合、適正な数値を求める一要素と考えて下さい。
また±2σ外の人は、実質4.55%しか存在しません。この値については統計上、無視をするという考え方も意味があります。上振れ下振れし過ぎている人は対象から外すというものです。特に低得点者のスコアについては、白紙答案等、真面目に解いていないために得られた値であったりしますので、項目分析の値に入れない方が真の値が判別しやすい事が挙げられます。
【2】偏差値
「偏差値」は、平均点が50点・標準偏差が10点になるように調整した時の、受験者のテストの点数を表しています。
偏差値においても、先の「68%。95%ルール」は利用できます。・偏差値60以上の人は、受験者全体の上位約16%に相当・偏差値70以上の人は、受験者全体の上位約2.3%に相当これは平均点に標準偏差を足した値が偏差値60になるわけですから、そうなるわけです。学校の全国テストで自分の子が偏差値70なんて取った日には、あなたは全国の生徒の2.3%以内に入る成績を取った天才だと褒めてあげて下さい。
【3】実質選択肢数
「実質選択肢数」は、実質的に機能している選択肢数を表します。この値は1~選択肢数の値で表現されます。
例えば全受験者が正解をした場合、値は1となります。つまり4択問題であるのに、実質は選択肢1個の問題を出していたという事になります。テストと呼ぶためには実質的に2以上の選択肢が機能しているべきですし、少なくとも1.5以上の値は出てほしい項目となります。この値が低い場合、有効な間違いの選択肢=錯乱肢を最低1個作り直す事を検討し、問題を作り直すのが良いと考えられます。
【4】合否判定力
「合否判定力」は、合格者通過率から不合格者通過率を差し引いた値を言います(通過率とは正答率の事です)。
試験問題が受験者の合否を判定する力の程度を示します。値は-1から1の値を取り、値が大きいほど、より合否判定力がある良い問題であるといえます。一般的には0.2以上の数値を取ることが望ましい状態であり、0.05以下の値については、合否判定力が低い(=即ち、合格者でも不合格者でも同じような通過率をとってしまう、もしくは受験者のレベルの低い方が良い点を取ってしまうような傾向が出た問題である)ことを示します。
「弁別指数」とほぼ同じ意味になります。弁別指数は上位27%と下位27%の受験者の通過率を比較し、その差を表したものになります。
こちらは対象母群の性質上、優劣の差が出やすいので0.3以上を良問の閾値とすべき値と言えます。「合否判定力」、「弁別指数」のどちらを利用すべきかはどちらでも良いと思います。
この指数はある基準で合格・不合格の判定をするテストに使うべき指標です。そのテストでは合格すべき人を合格に導き、不合格にすべき人を不合格になるように導くことがテストの設計として求められる最重要項目になります。
従って合否判定力が低い場合、合格判定するに相応しくない問題となりますので、そもそも出題する意味がありませんし、マイナスの値の問題を出題しますとむしろ合格すべき人を不合格に導いているという問題になります。ですので、利用方法としては、閾値を定め、閾値以上のものを採用、それ以外は見直しをかけて再登録をしていくと良いと思います。閾値を0.2にするのか、0.1にするのかは問題の質によって定めると良いでしょう。
全体の問題70%を活かしたいのであれば、合否判定力順に並べた上で上位70%の問題を採用し、それ以外は再検討をかけるといった利用方法が挙げられます。但し合否判定力であれば0.1以上、弁別指数であれば0.2以上に設定すべきです。それ以下であればかなり不適切な問題と考えるべきだからです。
【5】点双列相関係数
「点双列相関係数」は、受験者の総得点の高低と、ある1つの項目の高低(正誤)との関係を相関係数で示しています。
ある1つの項目でも受験者の総得点を予測する力が強いかどうかを判断できます。またこの値が大きい項目は、テストの総得点の高い受験者ほど正解し、総得点の低い受験者ほど不正解すると言えます。逆にこの値が小さい項目は、テストの総得点が高い受験者が不正解したにもかかわらず総得点が低い受験者が正解するなど、総得点に関係なくどの能力レベルでも、正解できる割合があまり変化しない項目であると考えられます。
一般的に、この値が0.400以上であれば良い項目と判断でき、0.200以下はあまり良い項目とは言えないと判断できます。この値については、合否判定力と同ようの扱いをすると良いと思いますが、点双列の方が数式的に精度が優れていると考えております(実際は異なる見解の値なので、比較することが的外れかもしれませんが)。
ですので、どちらかを使うならこちらの値を指標にして良いと思います。但し、弱点としては、サンプル受験者数が少ない場合や、そもそも受験者の母体がサンプルにそぐわない集団となっている場合は、相関関係を示している事が良いと言えないため、そういった場合には参考にすべき値ではないと考えられます。後述するテストの信頼性係数が高いテストであれば、この数値の信頼性は高くなる傾向にもなりますので、併せて利用すると良いと思います。
【6】信頼性係数
「信頼性係数」は、同一の個人に対して同一の条件のもとで同一のテストを繰り返し実施したとき、一貫して同一の得点が得られる程度をテスト得点の信頼性を示す指標として、0~1の間の値をとります。値が高ければ、非常に信頼性が高いテストであると言えます。
例えば、信頼性の高いテストで70点をとった受験者がもう一度同じテストを受けた場合(学習効果、測定誤差等は考慮しないものとすると)、ほぼ同じ70点をとるはずです。その信頼性を示す値がこの値となります。一般的にこの値が0.75以上であることが好ましいといわれています。
この値は項目数が多ければ大きくなり受験者集団によっても変化する性質があります。
テスト全体の信頼指標としては、この数値を利用するのが適正であり、この値が0.75や0.8といった基準を超えるテストを作成するべきです。主にクーロンバックのα信頼性係数という専門用語で使われますが、上記のような意味のものになります。
なお、テストの信頼性が低い場合、以下の4つのアイディアでより信頼性の高いテストを作成する事ができます。
- 項目数を増やす
- 各項目の分散を小さくする
- 合計点の分散を大きくする
- 後述の「この問題を削除した信頼性係数」にて悪い値の問題を削除する
【7】この問題を削除した信頼性係数
該当の試験よりその項目を削除した場合のテスト全体の信頼性を示します。
この問題を削除した場合にテストの信頼性が上がるという場合、その問題を出題する事でテストの信頼性を下げる事になります。この値は「試験全体の信頼性係数との差」として表現し、正の値は悪い項目になります。
本来、出題数が増えれば増える程、テストの信頼性は上がりますので、その問題を削除した方がテストの信頼性が上がるという事は、かなり良くない問題という事になります。
こちらの指標を元に各項目の良問・悪問判断をし、適正な問題セットを作成する事でテストの信頼性を上げる事が可能となります。
以上です。
今回は古典的テスト理論における代表的な分析結果の指標で出てくる値について、利用法について説明をさせていただきました。詳細の数式等はご説明しませんが、この値がどういった代物で、その値を元に何を考えれば良いのか?の参考にしていただければと思います。

